Spoon — My Mathematical Mind
 Album: Gimme Fiction
Album: Gimme FictionAvg rating:
Your rating:
Total ratings: 1669
Length: 5:02
Plays (last 30 days): 2
I wanna change your mind
Said I wanna set it right this time
I'm looking through you
You know who you are
And planning for the apocalypse
Is not considered
Considered cool
I don't suggest it myself
But no I won't sweat
I wanna change your ways
Said I'm gonna get it right one of these days
And I'm looking through you
Riding the brakes
Bringing about the apocalypse
Is not considered
Considered cool
Still you go setting it up
But never give it a thought
Just go setting it up
My mathematical mind can see the breaks
So I'm gonna stop riding the brakes
No no no no more ride the brakes
Instead I'm gonna see your stakes
Yeah I'm gonna see the stakes
Said I wanna set it right this time
I'm looking through you
You know who you are
And planning for the apocalypse
Is not considered
Considered cool
I don't suggest it myself
But no I won't sweat
I wanna change your ways
Said I'm gonna get it right one of these days
And I'm looking through you
Riding the brakes
Bringing about the apocalypse
Is not considered
Considered cool
Still you go setting it up
But never give it a thought
Just go setting it up
My mathematical mind can see the breaks
So I'm gonna stop riding the brakes
No no no no more ride the brakes
Instead I'm gonna see your stakes
Yeah I'm gonna see the stakes
Comments (175)add comment
sounds like soul coughing - screenwriters blues especially the beginning
Good tune!
easmann wrote:
It's true, maxjboxer, sexism in either direction is equally wrong. However quesarah made no comment at all about or against males. She or he reacted to an image someone else posted of a nature that is frequently used to marginalize or objectify women or otherwise to stereotype them as persons not to be taken seriously.
Also women have been subjected to millennia of, to put it mildly, unequal treatment, at the hands of men as a group, and have the right both to say so and to continue to try to level the to this day tilted cultural and economic playing fields. Males who complain about that appear selfish and resentful, if not worse.
Just as with racism, simply passing laws intended to ensure equality, or redress inequality, does not erase centuries of bias and injustice or correct unjust behavior, but it's a necessary step of progress.
Wikipedia: Legal rights of women in history
So how do we 'erase centuries of bias and injustice'? How do you change the past?
It's true, maxjboxer, sexism in either direction is equally wrong. However quesarah made no comment at all about or against males. She or he reacted to an image someone else posted of a nature that is frequently used to marginalize or objectify women or otherwise to stereotype them as persons not to be taken seriously.
Also women have been subjected to millennia of, to put it mildly, unequal treatment, at the hands of men as a group, and have the right both to say so and to continue to try to level the to this day tilted cultural and economic playing fields. Males who complain about that appear selfish and resentful, if not worse.
Just as with racism, simply passing laws intended to ensure equality, or redress inequality, does not erase centuries of bias and injustice or correct unjust behavior, but it's a necessary step of progress.
Wikipedia: Legal rights of women in history
So how do we 'erase centuries of bias and injustice'? How do you change the past?
h8rhater wrote:
Whomever down voted this is undoubtedly part of the problem being addressed by the comment.
So how do we erase centuries of bias and injustice? How do you change the past?
Whomever down voted this is undoubtedly part of the problem being addressed by the comment.
So how do we erase centuries of bias and injustice? How do you change the past?
Interesting. Love the outro.
Spooning sure sounds good
Spoon in Tokyo. LUCKY coloradojohn wrote:
When I heard "The Two Sides of Monsieur Valentine," I was intrigued by these guys...then, when I heard this -- also on RP as soon as it came out -- I WAS BLOWN AWAY! and when I saw them play a gig in Tokyo I was hooked on their wacky jamming ways. ROCK SOLID!
Superb. One of my favourite bands. Discovered here, so thanks RP.
easmann wrote:
It's true, maxjboxer, sexism in either direction is equally wrong. However quesarah made no comment at all about or against males. She or he reacted to an image someone else posted of a nature that is frequently used to marginalize or objectify women or otherwise to stereotype them as persons not to be taken seriously.
Also women have been subjected to millennia of, to put it mildly, unequal treatment, at the hands of men as a group, and have the right both to say so and to continue to try to level the to this day tilted cultural and economic playing fields. Males who complain about that appear selfish and resentful, if not worse.
Just as with racism, simply passing laws intended to ensure equality, or redress inequality, does not erase centuries of bias and injustice or correct unjust behavior, but it's a necessary step of progress.
Wikipedia: Legal rights of women in history
Whomever down voted this is undoubtedly part of the problem being addressed by the comment.
It's true, maxjboxer, sexism in either direction is equally wrong. However quesarah made no comment at all about or against males. She or he reacted to an image someone else posted of a nature that is frequently used to marginalize or objectify women or otherwise to stereotype them as persons not to be taken seriously.
Also women have been subjected to millennia of, to put it mildly, unequal treatment, at the hands of men as a group, and have the right both to say so and to continue to try to level the to this day tilted cultural and economic playing fields. Males who complain about that appear selfish and resentful, if not worse.
Just as with racism, simply passing laws intended to ensure equality, or redress inequality, does not erase centuries of bias and injustice or correct unjust behavior, but it's a necessary step of progress.
Wikipedia: Legal rights of women in history
Whomever down voted this is undoubtedly part of the problem being addressed by the comment.
first i liked spoon , now im super annoyed of this voice/style :/
Spoon, Just played Eugene spot on show! Especially this tune! thumbs up!
Absolutely in the top ten of the thousands of songs I have heard over the years on Radio Paradise.Simply brilliant.
marksda wrote:
If you don't mind my minding your language... Explaining mathematics — otherwise than with other mathematics — requires precision in whatever language you do choose to use to explain it.
The description above nearly conflates common failings: of lexical choice (e.g. the term "square" is being used to describe the method for calculating the length of the longest side of a right-angle triangle) and of precision (e.g. the sides of a triangle do not, from intuition or even observation, have "squares", and a 'side of a triangle' is not its length — length being an attribute of the referent side —, though the lengths of the sides of a triangle may be said to have "squares" once you have explained what it means to "square" a number)...
Don't Mind My Mathematics...
If you don't mind my minding your language... Explaining mathematics — otherwise than with other mathematics — requires precision in whatever language you do choose to use to explain it.
If you have a triangle with one perpendicular corner then you can add the squares of each side attached to that perpendicular corner to find the value of the square of the side opposite the perpendicular corner.
The description above nearly conflates common failings: of lexical choice (e.g. the term "square" is being used to describe the method for calculating the length of the longest side of a right-angle triangle) and of precision (e.g. the sides of a triangle do not, from intuition or even observation, have "squares", and a 'side of a triangle' is not its length — length being an attribute of the referent side —, though the lengths of the sides of a triangle may be said to have "squares" once you have explained what it means to "square" a number)...
lattalo wrote:
Both of you get an award for participation, even though only one of you is, technically, wrong. Isn't that great?!
Once you work out the correct numerical answer (hint: it isn't "42"), you'll never need to do the calculations ever again in the history of the universe. Also great, right?!
driver8 wrote:
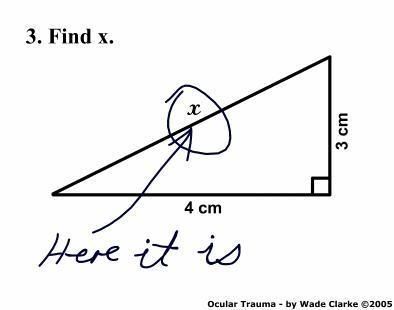 I had to figure this out, dusted off some cobwebs...
I had to figure this out, dusted off some cobwebs...

Both of you get an award for participation, even though only one of you is, technically, wrong. Isn't that great?!
Once you work out the correct numerical answer (hint: it isn't "42"), you'll never need to do the calculations ever again in the history of the universe. Also great, right?!
Billy Joel called. He wants his voice back.
Am totally fine with being spoon fed.
Great feel.
Great feel.
Vinni_NL wrote:
You lost me at "Triangle"


You lost me at "Triangle"
quesarah wrote:
maxjboxer wrote:
It's true, maxjboxer, sexism in either direction is equally wrong. However quesarah made no comment at all about or against males. She or he reacted to an image someone else posted of a nature that is frequently used to marginalize or objectify women or otherwise to stereotype them as persons not to be taken seriously.
Also women have been subjected to millennia of, to put it mildly, unequal treatment, at the hands of men as a group, and have the right both to say so and to continue to try to level the to this day tilted cultural and economic playing fields. Males who complain about that appear selfish and resentful, if not worse.
Just as with racism, simply passing laws intended to ensure equality, or redress inequality, does not erase centuries of bias and injustice or correct unjust behavior, but it's a necessary step of progress.
Wikipedia: Legal rights of women in history
Stupid. When is sexism going to be as unacceptable as racism?
Tired of girls/women being told they "can't" do something.
Tired of girls/women being told they "can't" do something.
maxjboxer wrote:
I agree. I am soo tired of boys/men being told they are just testosterone driven antagonists always on the verge of violent behavior twords women. There is no penalty for saying anything, no matter how offensive, about a man.
It's true, maxjboxer, sexism in either direction is equally wrong. However quesarah made no comment at all about or against males. She or he reacted to an image someone else posted of a nature that is frequently used to marginalize or objectify women or otherwise to stereotype them as persons not to be taken seriously.
Also women have been subjected to millennia of, to put it mildly, unequal treatment, at the hands of men as a group, and have the right both to say so and to continue to try to level the to this day tilted cultural and economic playing fields. Males who complain about that appear selfish and resentful, if not worse.
Just as with racism, simply passing laws intended to ensure equality, or redress inequality, does not erase centuries of bias and injustice or correct unjust behavior, but it's a necessary step of progress.
Wikipedia: Legal rights of women in history
Like it !
Second Spoon track of the afternoon and I am liking it!
I love spoon!
Some good comparisons here but this is Austin's very own Spoon....crunchy git and all....love to hear that others are enjoying them.
Man - I love this song - and Spoon in general. I like my guitars crunchy! 
I love how it lands on the major chord; I don't know of many songs that have this kind of minor->major thing going on. One time I was sitting at my keyboard just messing around, and happened to hit a low G octave with my left hand, and instantly heard this song pop in my head. I hit a G minor with my right hand, and from there it took me about 5 minutes to work out the rest of the song off the top of my head. Well, that was the left and right hands separately...I spent the next couple of hours trying to play them together.
Guitar sounds like Wilco
There's a Wings feeling in this song that completely blasts me. Can't figure out if that piano line has been programmed but it's actually quite difficult to play.
yeah, sounds good here too. Just found spoon this year with their new cd, I have had it in heavy rotation for a couple of weeks now.
Don't know of them at all, but really hits the spot, this time of day.
I would spoon with these guys
PSD time
Saw these guys in concert in a small theater in Ithaca a few weeks ago. One of the best shows I've ever seen! They were so much better than I'd expected. Just a great band!
Really fun song to play on the piano!
That 3-d version of the Pythagorean Theorem below kind of blew my mind...never heard anything like that. Going to have to test that for myself.
That 3-d version of the Pythagorean Theorem below kind of blew my mind...never heard anything like that. Going to have to test that for myself.
Love this one... it's my ringtone
What an awful time for PSD to not work.
quesarah wrote:
Stupid. When is sexism going to be as unacceptable as racism?
Tired of girls/women being told they "can't" do something.
richlister wrote:
I agree. I am soo tired of boys/men being told they are just testosterone driven antagonists always on the verge of violent behavior twords women. There is no penalty for saying anything, no matter how offensive, about a man.
Tired of girls/women being told they "can't" do something.
richlister wrote:
I agree. I am soo tired of boys/men being told they are just testosterone driven antagonists always on the verge of violent behavior twords women. There is no penalty for saying anything, no matter how offensive, about a man.
Pretty much over Spoon. All their stuff sounds the same. I like this one though
Spoon-ing is not just a name, it's an action...and chillin' at the same time.
It's comfortable..
It's comfortable..
Rockit wrote:
no just put it in the waste basket - it's past being done.
Put a fork in it!
no just put it in the waste basket - it's past being done.
When I heard "The Two Sides of Monsieur Valentine," I was intrigued by these guys...then, when I heard this -- also on RP as soon as it came out -- I WAS BLOWN AWAY! and when I saw them play a gig in Tokyo I was hooked on their wacky jamming ways. ROCK SOLID!
Put a fork in it!
richlister wrote:
More likely...
Dick, is that you?

More likely...
Dick, is that you?
Stupid. When is sexism going to be as unacceptable as racism?
Tired of girls/women being told they "can't" do something.
richlister wrote:
More likely...
Tired of girls/women being told they "can't" do something.
richlister wrote:

More likely...

More likely...
AHHHHHH!
Love this song!
Love this song!

Not a fan of this band, but this song has a great piano riff..... 

Just say Pythagoras
MaryAndrea wrote:
.....too.....
Who are them? This obsessive song made me stop my dinner to write this few words
.....too.....
Blastcat900 wrote:
8 for that crazy guitar
Yep.That's when I stopped what I was doing and started really listening. One would have to call whatever effect he or she is using...attention grabbing Good song. marksda wrote:
You lost me at "Triangle"
Don't Mind My Mathematics...
If you have a triangle with one perpendicular corner then you can add the squares of each side attached to that perpendicular corner to find the value of the square of the side opposite the perpendicular corner.
If you call the side opposite to the perpendicular corner "side C" then it does not matter which of the two remaining sides is called A or B. You are left with the following formula:
The length of side A squared plus the length of side B squared equals the length of side C squared.
(A x A) + (B x B) = (C x C)
Another way to write this is using the power symbol "^".
To square a number or bring it to a power of two is the same as if you simply multiply the number by itself.
So saying "B squared" is the same as saying "B times B", or saying "B to the power of two".
A^2 + B^2 = C^2
A way to visualize this is to imagine a square attached to each side of the triangle. The largest square, the one opposite the perpendicular corner, will always have an area equal in size to that of the combined area of the two smaller squares next to the perpendicular corner.
You can add the area of the two smaller squares to find the area of the biggest square, and the biggest square is always the furthest one from the perpendicular corner.
In the case where you have a triangle with sides next to the perpendicular corner having the length of 3 cm and 4 cm we can use the following equations:
(3 x 3) + (4 x 4) = (C x C)
9 + 16 = (C x C)
25 = (C x C)
What number when multiplied by itself equals 25?
The square root of 25 is C.
C equals 5.
So for this particular triangle, the length of the side opposite the perpendicular corner (the big side) is 5 cm long.
...
More complicated version:
Way back in 1999 I saw that if I held my index finger, middle finger, and thumb all in directions perpendicular to each other then they produced three triangles between each finger, and a fourth triangle (always the biggest) with corners defined by the three finger tips.
The three smaller triangles touch the perpendicular corner and all four triangles enclose a tetrahedron.
The area of the largest triangle is equal to the square root of the sum of the squares of the areas of the three smaller triangles.
If side a = 1 cm and side b = 2 cm and side c = 8 cm then,
area of triangle ab = (1*2)/2 = 1 square cm
area of triangle bc = (2*8)/2 = 8 square cm
area of triangle ca = (1*8)/2 = 4 square cm
area of big triangle = squareroot(1^2 + 8^2 +4^2) = 9 square centimeters
I'll spare you my mathematical proof for now.
If you have a triangle with one perpendicular corner then you can add the squares of each side attached to that perpendicular corner to find the value of the square of the side opposite the perpendicular corner.
If you call the side opposite to the perpendicular corner "side C" then it does not matter which of the two remaining sides is called A or B. You are left with the following formula:
The length of side A squared plus the length of side B squared equals the length of side C squared.
(A x A) + (B x B) = (C x C)
Another way to write this is using the power symbol "^".
To square a number or bring it to a power of two is the same as if you simply multiply the number by itself.
So saying "B squared" is the same as saying "B times B", or saying "B to the power of two".
A^2 + B^2 = C^2
A way to visualize this is to imagine a square attached to each side of the triangle. The largest square, the one opposite the perpendicular corner, will always have an area equal in size to that of the combined area of the two smaller squares next to the perpendicular corner.
You can add the area of the two smaller squares to find the area of the biggest square, and the biggest square is always the furthest one from the perpendicular corner.
In the case where you have a triangle with sides next to the perpendicular corner having the length of 3 cm and 4 cm we can use the following equations:
(3 x 3) + (4 x 4) = (C x C)
9 + 16 = (C x C)
25 = (C x C)
What number when multiplied by itself equals 25?
The square root of 25 is C.
C equals 5.
So for this particular triangle, the length of the side opposite the perpendicular corner (the big side) is 5 cm long.
...
More complicated version:
Way back in 1999 I saw that if I held my index finger, middle finger, and thumb all in directions perpendicular to each other then they produced three triangles between each finger, and a fourth triangle (always the biggest) with corners defined by the three finger tips.
The three smaller triangles touch the perpendicular corner and all four triangles enclose a tetrahedron.
The area of the largest triangle is equal to the square root of the sum of the squares of the areas of the three smaller triangles.
If side a = 1 cm and side b = 2 cm and side c = 8 cm then,
area of triangle ab = (1*2)/2 = 1 square cm
area of triangle bc = (2*8)/2 = 8 square cm
area of triangle ca = (1*8)/2 = 4 square cm
area of big triangle = squareroot(1^2 + 8^2 +4^2) = 9 square centimeters
I'll spare you my mathematical proof for now.
You lost me at "Triangle"
liking Spoon, this one and "Mystery Zone".
Shmelo wrote:
Ok! I like this song. I put an 8. Thank you Shmelo.
They are groove-pop-rock gods. All of their albums can be played front to back with little-to-no dull moments. A greatly underrated band. Also great to experience live.
Ok! I like this song. I put an 8. Thank you Shmelo.
They are groove-pop-rock gods. All of their albums can be played front to back with little-to-no dull moments. A greatly underrated band. Also great to experience live.
Who are them? This obsessive song made me stop my dinner to write this few words
8 for that crazy guitar
Cake with bigger amplifiers.
Blech.
Blech.
Spoon feed me please
First time I hear a song from spoon, like it alot.keep them coming bill ,more spoon please
listen_n_sf wrote:
Oh yeah we will! This isn't boring, however.
Saw a couple of local bands this past weekend, and the first act was REALLY LOUD, but boring. They compensated by swinging their very long hair around — in synch. Instantly changed from boring to highly amusing.
So if it's loud, no one will notice it's boring?
Oh yeah we will! This isn't boring, however.
Saw a couple of local bands this past weekend, and the first act was REALLY LOUD, but boring. They compensated by swinging their very long hair around — in synch. Instantly changed from boring to highly amusing.
Poacher wrote:
And you have a problem with that? Show me the rule that says all music must have a melody.
Your surprised Stingray doesn't get it?
And you have a problem with that? Show me the rule that says all music must have a melody.
Your surprised Stingray doesn't get it?
The more I hear of Spoon, the more I like! This really grabbed my attention, subtle but powerful.
GIMME more Spoon!
Poacher wrote:
And you have a problem with that? Show me the rule that says all music must have a melody.
Anyhow, this song has a "succession of single notes of varying pitch" - otherwise known as a "melody" - whether or not it's considered melodic or tuneful is something different.
And you have a problem with that? Show me the rule that says all music must have a melody.
Anyhow, this song has a "succession of single notes of varying pitch" - otherwise known as a "melody" - whether or not it's considered melodic or tuneful is something different.
Great friggin song!
listen_n_sf wrote:
it should be a 10
So if it's loud, no one will notice it's boring?
it should be a 10
Businessgypsy wrote:
Agreed. 9 in my book.
Whoa! This is awesome in every way. Love the lyric, pounding percussive melodic piano and that thrash guitar!
Agreed. 9 in my book.
Whoa! This is awesome in every way. Love the lyric, pounding percussive melodic piano and that thrash guitar!
Not bad!
I dig it.
Always like the spoon guitars
Always like the spoon guitars
So if it's loud, no one will notice it's boring?
Poacher wrote:
And you have a problem with that? Show me the rule that says all music must have a melody.
Official Rulebook of Music:
Rule #1: Blah, blah, blah
Rule #2: Blah, blah, blah
Rule #3: All songs must have a melody
Rule #4: Blah, blah, blah
Rule #5: If RP doesn't play it, it is not music
And you have a problem with that? Show me the rule that says all music must have a melody.
Official Rulebook of Music:
Rule #1: Blah, blah, blah
Rule #2: Blah, blah, blah
Rule #3: All songs must have a melody
Rule #4: Blah, blah, blah
Rule #5: If RP doesn't play it, it is not music
I love it when RP Spoons me!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
this is such an awesome, bad-ass, rocker of a song that i'm calling it my theme song
Radiohead + Spoon = lunchtime...later...
Stingray wrote:
And you have a problem with that? Show me the rule that says all music must have a melody.
No melody!
And you have a problem with that? Show me the rule that says all music must have a melody.
I'll take a bite from this spoon! 



Very nice!
parrothead wrote:
Very Good! As a mechanical engineer I some times must us formulas simular to your example. I must say, who gives a shit about the area of a triangle. It is very seldom used in modern design and testing. But I must admit, it makes me think about the days of my schooling thinking "when I'm I ever going to used this in the real world"
Here's one for you: The Angle of the dangle is proportionate to the heat of the meat over the mass of the ass.
Very Good! As a mechanical engineer I some times must us formulas simular to your example. I must say, who gives a shit about the area of a triangle. It is very seldom used in modern design and testing. But I must admit, it makes me think about the days of my schooling thinking "when I'm I ever going to used this in the real world"
Here's one for you: The Angle of the dangle is proportionate to the heat of the meat over the mass of the ass.
parrothead wrote:
Very Good! As a mechanical engineer I some times must us formulas simular to your example. I must say, who gives a shit about the area of a triangle. It is very seldom used in modern design and testing. But I must admit, it makes me think about the days of my schooling thinking "when I'm I ever going to used this in the real world"
I r a injuneer, to.
Very Good! As a mechanical engineer I some times must us formulas simular to your example. I must say, who gives a shit about the area of a triangle. It is very seldom used in modern design and testing. But I must admit, it makes me think about the days of my schooling thinking "when I'm I ever going to used this in the real world"
I r a injuneer, to.
No melody!
marksda wrote:
Very Good! As a mechanical engineer I some times must us formulas simular to your example. I must say, who gives a shit about the area of a triangle. It is very seldom used in modern design and testing. But I must admit, it makes me think about the days of my schooling thinking "when I'm I ever going to used this in the real world"
Don't Mind My Mathematics...
If you have a triangle with one perpendicular corner then you can add the squares of each side attached to that perpendicular corner to find the value of the square of the side opposite the perpendicular corner.
If you call the side opposite to the perpendicular corner "side C" then it does not matter which of the two remaining sides is called A or B. You are left with the following formula:
The length of side A squared plus the length of side B squared equals the length of side C squared.
(A x A) + (B x B) = (C x C)
Another way to write this is using the power symbol "^".
To square a number or bring it to a power of two is the same as if you simply multiply the number by itself.
So saying "B squared" is the same as saying "B times B", or saying "B to the power of two".
A^2 + B^2 = C^2
A way to visualize this is to imagine a square attached to each side of the triangle. The largest square, the one opposite the perpendicular corner, will always have an area equal in size to that of the combined area of the two smaller squares next to the perpendicular corner.
You can add the area of the two smaller squares to find the area of the biggest square, and the biggest square is always the furthest one from the perpendicular corner.
In the case where you have a triangle with sides next to the perpendicular corner having the length of 3 cm and 4 cm we can use the following equations:
(3 x 3) + (4 x 4) = (C x C)
9 + 16 = (C x C)
25 = (C x C)
What number when multiplied by itself equals 25?
The square root of 25 is C.
C equals 5.
So for this particular triangle, the length of the side opposite the perpendicular corner (the big side) is 5 cm long.
...
More complicated version:
Way back in 1999 I saw that if I held my index finger, middle finger, and thumb all in directions perpendicular to each other then they produced three triangles between each finger, and a fourth triangle (always the biggest) with corners defined by the three finger tips.
The three smaller triangles touch the perpendicular corner and all four triangles enclose a tetrahedron.
The area of the largest triangle is equal to the square root of the sum of the squares of the areas of the three smaller triangles.
If side a = 1 cm and side b = 2 cm and side c = 8 cm then,
area of triangle ab = (1*2)/2 = 1 square cm
area of triangle bc = (2*8)/2 = 8 square cm
area of triangle ca = (1*8)/2 = 4 square cm
area of big triangle = squareroot(1^2 + 8^2 +4^2) = 9 square centimeters
I'll spare you my mathematical proof for now.
If you have a triangle with one perpendicular corner then you can add the squares of each side attached to that perpendicular corner to find the value of the square of the side opposite the perpendicular corner.
If you call the side opposite to the perpendicular corner "side C" then it does not matter which of the two remaining sides is called A or B. You are left with the following formula:
The length of side A squared plus the length of side B squared equals the length of side C squared.
(A x A) + (B x B) = (C x C)
Another way to write this is using the power symbol "^".
To square a number or bring it to a power of two is the same as if you simply multiply the number by itself.
So saying "B squared" is the same as saying "B times B", or saying "B to the power of two".
A^2 + B^2 = C^2
A way to visualize this is to imagine a square attached to each side of the triangle. The largest square, the one opposite the perpendicular corner, will always have an area equal in size to that of the combined area of the two smaller squares next to the perpendicular corner.
You can add the area of the two smaller squares to find the area of the biggest square, and the biggest square is always the furthest one from the perpendicular corner.
In the case where you have a triangle with sides next to the perpendicular corner having the length of 3 cm and 4 cm we can use the following equations:
(3 x 3) + (4 x 4) = (C x C)
9 + 16 = (C x C)
25 = (C x C)
What number when multiplied by itself equals 25?
The square root of 25 is C.
C equals 5.
So for this particular triangle, the length of the side opposite the perpendicular corner (the big side) is 5 cm long.
...
More complicated version:
Way back in 1999 I saw that if I held my index finger, middle finger, and thumb all in directions perpendicular to each other then they produced three triangles between each finger, and a fourth triangle (always the biggest) with corners defined by the three finger tips.
The three smaller triangles touch the perpendicular corner and all four triangles enclose a tetrahedron.
The area of the largest triangle is equal to the square root of the sum of the squares of the areas of the three smaller triangles.
If side a = 1 cm and side b = 2 cm and side c = 8 cm then,
area of triangle ab = (1*2)/2 = 1 square cm
area of triangle bc = (2*8)/2 = 8 square cm
area of triangle ca = (1*8)/2 = 4 square cm
area of big triangle = squareroot(1^2 + 8^2 +4^2) = 9 square centimeters
I'll spare you my mathematical proof for now.
Very Good! As a mechanical engineer I some times must us formulas simular to your example. I must say, who gives a shit about the area of a triangle. It is very seldom used in modern design and testing. But I must admit, it makes me think about the days of my schooling thinking "when I'm I ever going to used this in the real world"
jkhandy wrote: Why such a low avg.?
Why such a low avg.?
Because the song is mediocre. Not bad, but certainly not great.
Because the song is mediocre. Not bad, but certainly not great.
Yea, it is confirmed now, this IS my favorite Spoon tune!!

Rhythm with out importance, I will take it! and then some more...modern day Punk!!! like it!
peter_james_bond wrote:
Oh, yeah, the cross-over between music and math is well-known and I know I'm not the only RP commenter who's a former musician now working in computer science. Of my four-person team here at work, two of us are former musicians and a third is an arts major who worked in music production for ages before coming into CS.
If you want your mind blown, though, look into the Bohlen-Pierce system, which is a 13-tone system where the top note is triple the frequency of the low note and the interval is divided by 13.
Here's an excellent recent write-up:
https://www.boston.com/bostonglobe/ideas/articles/2010/03/07/symphony_in_j_flat/
Spoon is on to something, check this out:
Music and mathematics
Oh, yeah, the cross-over between music and math is well-known and I know I'm not the only RP commenter who's a former musician now working in computer science. Of my four-person team here at work, two of us are former musicians and a third is an arts major who worked in music production for ages before coming into CS.
If you want your mind blown, though, look into the Bohlen-Pierce system, which is a 13-tone system where the top note is triple the frequency of the low note and the interval is divided by 13.
Here's an excellent recent write-up:
https://www.boston.com/bostonglobe/ideas/articles/2010/03/07/symphony_in_j_flat/
wow i love this this band....do not hear them enough!
Probably my favorite Spoon Tune!
Spoon...they stir up and then dish out a heaping helping of delicious Rock'n'Roll for us to scarf down.  Ahhh, you've got some on the side of your mouth...no the other side...no higher...there ya go.
Ahhh, you've got some on the side of your mouth...no the other side...no higher...there ya go. 
HOLY CRAP! Its only 5.99 on Amazon.com as MP3 Album download !!!

now downloading, amazon mp3's at less than 6 bucks .... gotta love the internet and RadioParadise! Thanks Bill :)

now downloading, amazon mp3's at less than 6 bucks .... gotta love the internet and RadioParadise! Thanks Bill :)
Nice!!
Hope you've read "Wicked. Pretty amazing take on the Oz story. Doesn't, however, delve into the Pythagorean theorem that I recall.
rharvey658 wrote:
Actually, if you listen closely to the Scarecrow, he says the sum of the 'square-roots' of two sides equals the 'square-root' of the remaining side, which is not correct, at least in our universe. So, my conclusion is that Dorothy had actually traveled to a different universe, where simple rules like pythagoras, and gravity (flying on a broom ?) are quite different from here.
rharvey658 wrote:
Actually, if you listen closely to the Scarecrow, he says the sum of the 'square-roots' of two sides equals the 'square-root' of the remaining side, which is not correct, at least in our universe. So, my conclusion is that Dorothy had actually traveled to a different universe, where simple rules like pythagoras, and gravity (flying on a broom ?) are quite different from here.
I'll say it again......bloody genius
What a night — watchin' the world series — listening to RP — it just doesn't
get any better !!! —- oh ya then there's the brew —- HAPPY HALLOWEEN
TO YOU ALL — THANKS FOR A KICK ASS NIGHT of R&R BILL !!
I truly believe this album is destined for classic status. Amazing stuff.
Too noisy, particularly at the end
Spoon is on to something, check this out:
Music and mathematics
rharvey658 wrote:
Hmmm, very observant. I'm gonna pay more attention next time I see that scene. In a world where monkeys fly . . .
Actually, if you listen closely to the Scarecrow, he says the sum of the 'square-roots' of two sides equals the 'square-root' of the remaining side, which is not correct, at least in our universe. So, my conclusion is that Dorothy had actually traveled to a different universe, where simple rules like pythagoras, and gravity (flying on a broom ?) are quite different from here.
Hmmm, very observant. I'm gonna pay more attention next time I see that scene. In a world where monkeys fly . . .
FlamingLotus wrote:
Yes, much better than anything else I've heard by them.
First Spoon song I've heard that I like...
Yes, much better than anything else I've heard by them.
 <== Click for Netflix link
<== Click for Netflix linkThis jarring black-and-white brain-bender is a haunting examination of science — and obsession. Written and directed by Darren Aronofsky (Requiem for a Dream), Pi: Faith in Chaos tells the story of a haunted, fragile mathematical genius (Sean Gullette) on the trail of a 216-digit number hidden in Pi that could unlock the secrets of the stock market ... and the universe.
Never heard of this band before .... outstanding; would love to hear more!
The New Math  Spoon + My ears =
Spoon + My ears = 
Nice thrashing guitars
Reminds me of the Mother Hips. (Hint, Hint Bill) 8
Bang those bones boy!!!


philbertr wrote:
I am old as dirt and this CD (my first exposure to Spoon) was like a breath of fresh air - not one lame cut on the whole deal - since then i have listened to a lot of their stuff and it keeps changing and I like all of it - excellent in concert also. their drummer quit his day job last year as a chip designer - their percussion is very inventive
rock on

Can anyone comment on the rest of the album? This cut is fantastic!
I am old as dirt and this CD (my first exposure to Spoon) was like a breath of fresh air - not one lame cut on the whole deal - since then i have listened to a lot of their stuff and it keeps changing and I like all of it - excellent in concert also. their drummer quit his day job last year as a chip designer - their percussion is very inventive
rock on
I just want to say that rp's hitting it on all cylinders tonight.
Can anyone comment on the rest of the album? This cut is fantastic!

First Spoon song I've heard that I like...
wotta band!

This makes the second Spoon song I've liked a lot (the other being 'Don't You Evah').
I might just have to buy some of their stuff!
araja wrote:
Dude. The Scarecrow in Wizard of Oz discribed this same thing in one line!
Actually, if you listen closely to the Scarecrow, he says the sum of the 'square-roots' of two sides equals the 'square-root' of the remaining side, which is not correct, at least in our universe. So, my conclusion is that Dorothy had actually traveled to a different universe, where simple rules like pythagoras, and gravity (flying on a broom ?) are quite different from here.
Dude. The Scarecrow in Wizard of Oz discribed this same thing in one line!
Actually, if you listen closely to the Scarecrow, he says the sum of the 'square-roots' of two sides equals the 'square-root' of the remaining side, which is not correct, at least in our universe. So, my conclusion is that Dorothy had actually traveled to a different universe, where simple rules like pythagoras, and gravity (flying on a broom ?) are quite different from here.
lattalo wrote:
I had to figure this out, dusted off some cobwebs.
sql root of x = 3*3 + 2*2
3.61 cm
God am I bored!!!!!!!
 sqrt x = 3*2 + 4*2, which is 9 + 16, which is 25, therefore x=5, not 3.61.
sqrt x = 3*2 + 4*2, which is 9 + 16, which is 25, therefore x=5, not 3.61.
And, of course, it was actually a joke (Find x - here it is!)
Sorry for the grumpfest, been up and working since 445am.
I had to figure this out, dusted off some cobwebs.
sql root of x = 3*3 + 2*2
3.61 cm
God am I bored!!!!!!!
And, of course, it was actually a joke (Find x - here it is!)
Sorry for the grumpfest, been up and working since 445am.

marksda wrote:
Seeing as you have so much time Pythagoras, would you mind doing my laundry.
Don't Mind My Mathematics... If you have a triangle with one perpendicular corner then you can add the squares of each side attached to that perpendicular corner to find the value of the square of the side opposite the perpendicular corner. If you call the side opposite to the perpendicular corner "side C" then it does not matter which of the two remaining sides is called A or B. You are left with the following formula: The length of side A squared plus the length of side B squared equals the length of side C squared. (A x A) + (B x B) = (C x C) Another way to write this is using the power symbol "^". To square a number or bring it to a power of two is the same as if you simply multiply the number by itself. So saying "B squared" is the same as saying "B times B", or saying "B to the power of two". A^2 + B^2 = C^2 A way to visualize this is to imagine a square attached to each side of the triangle. The largest square, the one opposite the perpendicular corner, will always have an area equal in size to that of the combined area of the two smaller squares next to the perpendicular corner. You can add the area of the two smaller squares to find the area of the biggest square, and the biggest square is always the furthest one from the perpendicular corner. In the case where you have a triangle with sides next to the perpendicular corner having the length of 3 cm and 4 cm we can use the following equations: (3 x 3) + (4 x 4) = (C x C) 9 + 16 = (C x C) 25 = (C x C) What number when multiplied by itself equals 25? The square root of 25 is C. C equals 5. So for this particular triangle, the length of the side opposite the perpendicular corner (the big side) is 5 cm long. ... More complicated version: Way back in 1999 I saw that if I held my index finger, middle finger, and thumb all in directions perpendicular to each other then they produced three triangles between each finger, and a fourth triangle (always the biggest) with corners defined by the three finger tips. The three smaller triangles touch the perpendicular corner and all four triangles enclose a tetrahedron. The area of the largest triangle is equal to the square root of the sum of the squares of the areas of the three smaller triangles. If side a = 1 cm and side b = 2 cm and side c = 8 cm then, area of triangle ab = (1*2)/2 = 1 square cm
area of triangle bc = (2*8)/2 = 8 square cm
area of triangle ca = (1*8)/2 = 4 square cm area of big triangle = squareroot(1^2 + 8^2 +4^2) = 9 square centimeters I'll spare you my mathematical proof for now.
area of triangle bc = (2*8)/2 = 8 square cm
area of triangle ca = (1*8)/2 = 4 square cm area of big triangle = squareroot(1^2 + 8^2 +4^2) = 9 square centimeters I'll spare you my mathematical proof for now.
Seeing as you have so much time Pythagoras, would you mind doing my laundry.
This ROCKS!!!
8 => 9




So how do we erase centuries of bias and injustice? How do you change the past?
You don't - wrong question. You create a future based on wisdom from the past.